Správne riešenia úloh z Lekcie 3
Na úvod riešenia úloh 8-12, bodované časti sú hrubým písmom. Dostali sme pripomienku, aby boli zverejňované aj mená autorov. Toto je štandardný postup, vždy keď sa niekde uvádza úloha, malo by pri nej byť aj meno autora, prípadne rok vydania a časopis alebo udalosť, na ktorej sa objavila. Ja som na to však pri riešeniach súťažných úloh zabudol, za čo sa ospravedlňujem, mená boli doplnené v článkoch pri riešeniach úloh.
 |
G. Heathcote, Reading Observer, 1904
1. Ja2 zz |
 |
F. Giegold, Stern, 1965 1. Dh2 zz 1…g2 2. Sb8+ (1.5) 1…gxh2 2. Sxh2 (1.5) |
 |
G. Anderson, BCF 17 Ty, 2.cena 1. Dg6 (2.Dg3+) (1) 1…Sxg6 2. Jg4+ (1) 1…Sg4 2. Jxg4+/e3 (1) 1…Sxd3 2. Jxd3 (1) 1…Kxd4 2. Db6+ (1) 1…d6 2. e3 (1) |
 |
W. Shinkman, Holyoke Transcript, 1881, 1.cena 1. Dh5 (2. Dd1#) 1…Je2 2. Jc5+ (2) 1…Jxh5 2. Jc6 (2) 1…c3 2. Ka2 (2) |
 |
P. Copping, The Guardian, 1962 1. Df1 (2. Vxe6+) (1) 1…gxf1~ 2. Jb4 (3) 1…Vf2 2. Jb4 (2) 1…Sd8 2. Vxe6+ Kxe6 3. Vc6# |
Štúdie – domáca pôda
Od trochu predĺženej lekcie trojťažiek sa dostávame hneď k najťažšiemu oddeleniu – štúdiam. Štúdie sú však zároveň typom úlohy, ktorý je praktickému šachistovi najbližší a takmer každý šachista sa v živote už určite s nejednou štúdiou stretol. Napriek tomu, že sú nám štúdie dôverne známe, začnem tým, čo to vlastne tá štúdia je.
Definícia dvojťažky je jednoduchá – je to pozícia, v ktorej má biely jediný ťah taký, že na každú odpoveď čierneho príde mat ďalším ťahom. Samozrejme, podmienku, že úvodník je jediný by sme mohli pokojne aj vypustiť – stačí, že biely vie vynútiť mat druhým ťahom. Nám však ide aj o istú estetickú hodnotu, a teda chceme, aby bolo riešenie jednoznačné.
Podobne by sme mohli skúsiť definovať aj trojťažku alebo dlhšiu úlohu. Tu sa však už občas stáva, že ďalšie ťahy bieleho sú nejednoznačné a napriek tomu je úloha stále pekná. Môžeme teda vyžadovať jednoznačnosť v prvom ťahu bieleho, ale ďalej nám už stačí, že existuje nejaké pokračovanie.
Definícia štúdie
Všetky tieto úlohy sú však ešte stále ohraničené počtom ťahov. Ako definovať štúdiu, teda úlohu, ktorá je vo svojej podstate neohraničená? Je to ľubovoľná pozícia, v ktorej biely na ťahu vyhrá/remizuje? Mohla by byť, ale to sa nezdá ako priveľmi užitočná definícia. Z môjho pohľadu je štúdia taká pozícia, v ktorej má biely jediný ťah taký, že existuje ťah čierneho taký, že biely má jediný ťah, …, taký, že biely vyhrá/remizuje, pričom táto reťaz sa končí vtedy, keď už čierny nemá takú odpoveď, aby vynútil jediný ťah bieleho. Rozoberme si, čo sa tým chce vlastne povedať.
Jediné ťahy bieleho – to je rovnaké ako pri priamych úlohách. Teraz však vyžadujeme jednoznačnosť až do konca. To, že existuje vždy ťah čierneho, ktorý vynucuje jediný ťah bieleho, znamená, že čierny má akési „najlepšie obrany“. Nejde o to, že by tieto ťahy naozaj pomohli čiernemu zachrániť sa, ale vyžadujú od bieleho najväčšiu možnú dávku presnosti. A v praktickej partii to môže naozaj znamenať rozdiel vo výsledku. No a nakoniec máme podmienku, kedy sa štúdia považuje za vyriešenú. Pravidlom totiž je, že každý ťah bieleho v štúdii musí byť jednoznačný. Pokiaľ sa už teda čierny nevie brániť tak, že vynucuje jednoznačné ťahy bieleho, riešenie nemôže ďalej pokračovať.
Toto „zastavovacie kritérium“ je možno vhodné pre definíciu, ale keď riešime, je užitočnejšie overiť si aj inú skutočnosť, a to, že výsledná pozícia je očividne vyhratá/remízová. Štúdia zvyčajne končí matom, patom, večným šachom alebo ziskom rozhodujúceho materiálu.
Bodovanie štúdií
Načo toľko rečí okolo toho celého? Pretože je to dôležité pri písaní riešenia. Objasnime si najprv, ako sú štúdie bodované. Každá štúdia má takzvanú hlavnú variantu, teda postupnosť ťahov bieleho a odpovedí čierneho, ktorá vyústi do vyhratej/remízovej pozície. Túto hlavnú variantu určuje autor štúdie, prípadne rozhodca súťaže a úlohou riešiteľa je nájsť ju. Nič iné sa v úlohe neboduje. Nie je teda potrebné písať po každom ťahu bieleho všetky obrany čierneho, stačí nájsť tú najsilnejšiu a pokračovať ňou. Hlavná varianta pozostáva iba z najsilnejších obrán.
Čo však v prípade, keď má čierny viac najsilnejších obrán, teda ťahov, ktoré vynucujú jednoznačnú odpoveď bieleho? V takom prípade treba napísať všetky. Nie preto, že by sa bodovali, ale preto, že nemáme ako vedieť, ktorá z variant sa bodovať bude. V niektorých prípadoch je to zrejmé – môžeme to vidieť podľa toho, po ktorej obrane je umožnený nejaký pekný obrat, prípadne ktorá obrana podsúva bielemu nejakú pascu. Niekedy je to však ťažké a na každej súťaži sa množstvo riešiteľov popáli na tom, že nenapísali nejakú variantu, lebo si mysleli, že určite nie je hlavná.
Čo sa týka samotného delenia bodov (v našom prípade je každá štúdia za najviac 10 bodov), hlavná varianta sa boduje po častiach, akýchsi „checkpointoch“. Sú teda vybrané niektoré ťahy z hlavnej varianty, za ktoré dostaneme predpísaný počet bodov a čím väčšiu časť štúdie máme správne, tým viac bodov dostaneme. Tieto ťahy sú zvyčajne tie náročné, teda také, kde dochádza k nejakému nečakanému obratu. Zvyčajne je 0,5 alebo 1 bod už aj za úvodník alebo za sériu zopár úvodných ťahov, oplatí sa teda hádať ak aj nevieme celé riešenie. Pravidlom je, že bodované sú vždy iba ťahy bieleho, avšak správne musia byť samozrejme aj ťahy čierneho.
Takže rekapitulácia. Štúdia je taká úloha, v ktorej biely na ťahu buď vyhrá alebo remizuje. Cieľ sa dosahuje reťazou jediných ťahov bieleho a najsilnejších odpovedí čierneho, pričom vieme, že úloha je vyriešená, ak už čierny nemá najsilnejšie obrany a zároveň je pozícia očividne vyhratá/remízová. Na kontrolu správnosti si musíme overiť, či sme našli v našej hlavnej variante nejaký pekný motív – obranu pomocou patu, obeť figúry, neprijatie obete figúry a podobne. A potom napísať do riešenia čo najviac aj bočných variánt (samozrejme iba tam, kde môže nastať nejaká pochybnosť).
Riešenie štúdií
No dobre, ale ako teda nájsť riešenie štúdie? Podobne, ako keď hráme partiu – snažíme sa jednoducho hľadať najlepšie ťahy. Pri tom sa môžeme riadiť pravidlom o jednoznačnosti – keď sa zrazu zdá, že biely má príliš veľa rovnocenných ťahov na výber, je to signál, že sme zišli z cesty.
Musíme tiež myslieť na to, že sa musí vyskytnúť nejaký pekný motív. Keď hráme na výhru, často sa čierny zachraňuje pomocou patu a my to musíme nejako prekonať (napríklad niečo najprv obetovať). Iný motív je napríklad, že v úvodnej pozícii sú naše figúry napadnuté a musia nejakým nečakaným spôsobom utiecť. V remízových štúdiach sa zase naopak biely často snaží zachrániť patom. Medzi ďalšie motívy patrí chytanie ďaleko postúpeného pešiaka na jednej či druhej strane, ale napríklad aj chytanie súperových figúr. Chytaný je väčšinou jazdec, ale existujú aj veľmi pekné štúdie, ktoré končia napríklad chytením súperovej veže či dámy hoc aj v strede šachovnice. Toto je samozrejme veľmi ťažké vidieť dopredu, ale oplatí sa to mať na pamäti, najmä keď vidíme, že súperova figúra (a môže to byť naozaj hociktorá) má pokryté množstvo ústupových polí alebo nejako obmedzenú pohyblivosť.
Pri riešení je tiež užitočné uvedomiť si, že skladateľ, keď skladal úlohu, musel ju skladať tak, aby si bol aspoň viac-menej istý, že je korektná. Prepočet variant teda zvyčajne nie je extrémne náročný a pokiaľ sa nám zdá, že nejakú variantu nevieme dopočítať ani po 10 ťahoch, asi to nebude riešenie. Hlavná varianta zvyčajne neobsahuje príliš hlboký prepočet.
Množstvo štúdií začína pozíciou „in medias res“, teda takou, kde je jedna zo strán (alebo dokonca aj obe) pod veľkým počtom hrozieb a treba rýchlo konať a odvracať nejako hrozby. Príkladom môže byť pešiak na siedmej rade, ktorého proste treba nejako chytať, či odkrytý kráľ proti presile súperových figúr alebo množstvo visiacich kameňov. Veľmi často je úvodníkom šach alebo branie figúry (ale častejšie šach) a nepovažuje sa to za nedostatok. Takýmto spôsobom si skladateľ overuje, že úvodná pozícia naozaj vyžaduje od bieleho jediný ťah. Dosť už ale všeobecných rečí, poďme sa pozrieť, ako takú štúdiu riešiť.
Poznámka: ilustračné príklady sú prebrate z knihy P. Murdziu, Rozwiazuj z Mistrzem Swiata, štúdie na výhru označujeme symbolom +, štúdie na remízu symbolom =, pokiaľ nie je uvedené inak, vždy je na ťahu biely.
J.Fritz, Gros, 1938, +
Tak, ako v poslednej lekcii, aj teraz sa pokúsim priblížiť svoj autentický myšlienkový pochod. Môžeme si všimnúť, že pri danom materiáli je bieleho jedinou šancou na výhru pešiak, ale na ťah c7 prichádza dvojitý úder Sf4+. Zároveň Sf4 funguje aj ako hrozba zo strany čierneho – za pešiaka môže strelca pokojne aj obetovať. Prirodzene teda vyskúšame pokryť pole f4 a pohroziť postupom c7. Možnosti sú dve, no po hlbšom preskúmaní zistíme, že Je6 Sb2 nevyzerá veľmi sľubne – nevieme už zabrániť strelcovi v presune na diafonálu h2-b8. Skúsme teda ťah 1. Kg3. Prirodzenou odpoveďou čierneho je Sb2 alebo Sa3, avšak na to má biely Jf7+ s pokrytím polí d6 a e5 a následným nezabrániteľným c7. Zdá sa zrazu, že čierny už nemá čo proti c7 urobiť. Toto je počas riešenia štúdií bežné – nevedieť nájst najsilnejšiu obranu čierneho. To zvyčajne znamená, že je buď varianta zlá alebo prichádza zvrat. Tak je to aj v našom prípade a konkrétne, čierny môže hrať 1…Jb4 s myšlienkou vidličky na d5 po prilákaní kráľa na f4 ťahom Sf4.
Opäť sa zdá, že sme narazili – biely pešiak visí a jediný spôsob ako ho zachrániť vedie iba k spomínanej vidličke. Môžeme si však všimnúť, že jazdec bude po vidličke zatiahnutý ku kraju šachovnice a možno sa ho bude dať chytiť. Skúsme teda 2. c7 Sf4+ 3. Kxf4 Jd5+ 4. Ke5 Jxc7 5. Kd6. Ústup na a8 samozrejme nič nerieši, takže vynútené je 5…Je8. Pokiaľ nechceme dovoliť jazdcovi újsť na f6, musíme hrať 6. Ke7. Návrat na c7 už nie je možný pre Kd7, opäť vynútené je teda 6…Jg7. Tým sa zdá, že sme skončili, jazdec je v bezpečí pri kráľovi a už ho nechytíme. Nie je to však celkom tak, pretože znovu prichádza zvrat 7. Kf8! a čierny je v zugzwangu. Kráľ sa nemôže hýbať, lebo stratí jazdca a jazdec má jediný ústup na h5, po ktorom prichádza Jf7#.
Ako ste mohli vidieť, štúdia nebola príliš komplikovaná, ťahy boli v podstate vynútené, niektoré alternatívne pokračovania sa dali ľahko vylúčiť. Jediná zrádnosť spočíva v tom, že keď prepočítavame variantu a aj nám napadne myšlienka s chytaním jazdca, sme náchylní počítať iba do Je8 a potom už vidíme, že jazdec sa dostane do bezpečia na g7 a variantu zahodíme. Pokiaľ prepočítavame dlhú variantu, ktorá je vynútená, neradno sa vzdávať príliš rýchlo – takéto varianty sú často riešením alebo takmer riešením (s tým, že treba napríklad ešte vsunúť nejaký ťah). Dlhá postupnosť vynútených ťahov je okrem toho, keď nájdeme nejaký veľmi pekný motív, najlepším vodítkom.
J.Rusinek, Problem, 1974-75, 1.cena, =
Ako druhý príklad uvedieme remízovú štúdiu. Biely čelí veľkej materiálnej prevahe a jeho jedinou nádejou je pešiak, takže nie je veľmi na čo čakať – 1.b6. Teraz hrozí v prvom rade b7, ale aj Vxf3 s ďalším b7. V dôsledku týchto hrozieb je čierny donútený hrať 1…Vf5 (aby na f3 vedel dobrať vežou). Podobne ako v minulej štúdii, čierny síce našu hrozbu pokryl, no my v nej aj tak pokračujeme – 2.b7. Toto je všeobecne častý motív štúdií – hrozba sa vykoná aj napriek tomu, že jej bolo zabránené. V našej pozícii na to môžeme prísť tak, že vlastne iné rozumné ťahy ani veľmi nemáme. Čierny samozrejme odpovedá 2…Vf7+ a ak nechceme pešiaka stratiť len tak, musíme napadnúť jazdca 3.Kd6. Teraz hrozí premena a Jc6 ani Jd7 nejde kvôli Vxf3, neostáva teda nič iné ako 3…Jc4+. Teraz máme síce na výber dva ústupy, ale keďže po Kc4 Vc7+ s ďaším Sb7 rýchlo prehrávame, vynútené je 4. Ke6. Teraz visia obe veže a čierny si už môže – a aj musí – dovoliť vziať pešiaka strelcom (vežou nie, lebo visí strelec), 4…Sxb7. Vežu dobrať nemôžeme, čo ostáva iné ako dať šach, 5.Vh3+ Kg7 6. Vg3+ Kf8. Teraz si už len stačí uvedomiť, že biely kráľ vlastne stojí v pate a riešenie je hotové: 7.Vg8+!=.
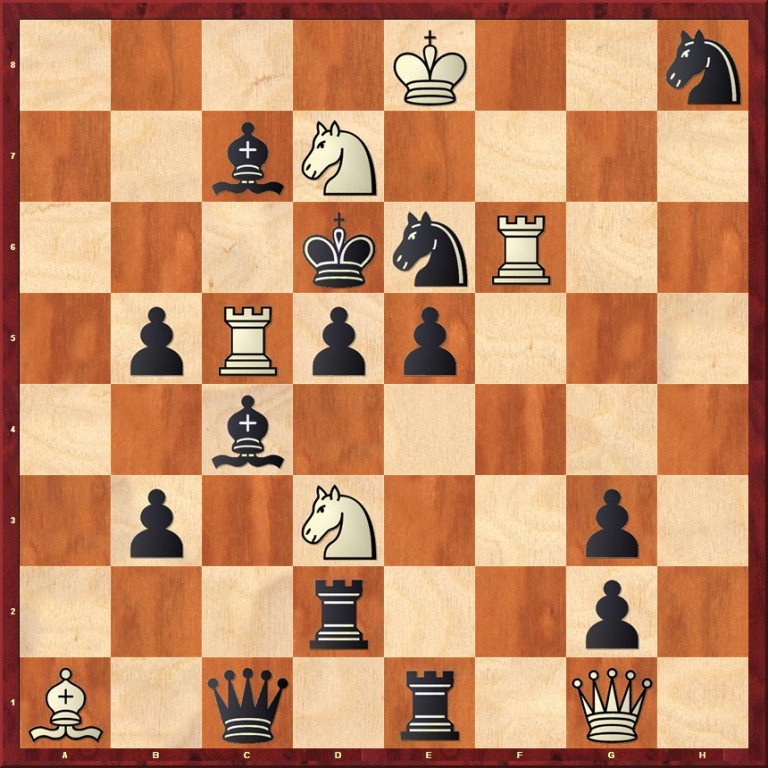
Súťažná úloha č. 13
Biely na ťahu vyhrá. Úloha za max. 10 bodov.
Súťažná úloha č. 14
Biely na ťahu remízuje. Úloha za max. 10 bodov.
Súťažná úloha č. 15
Biely na ťahu remízuje. Úloha za max. 10 bodov.
Súťažná úloha č. 16
Biely na ťahu vyhrá
Riešenia z Lekcie 4 poslané do 3.7.2016 23:59 budú započítané do súťaže.
Riešenie pošli formulárom nižšie. Nezabudni napísať číslo súťažnej úlohy.
[contact-form-7 id=“4084″ title=“Kompozičný šach“]
Tréningové šachové DVD
Partneri súťaže
Priebežné poradie po Lekcii č.3 # Nick Počet bodov PH1 OndrejFranko 44 34 Jozef 44 38 janjurco 44 69 Bohuslav Czudek 44 71 Milan Svrček 43 108 Peter Lukáč 40 114 PaeDr. Ján Husák 32 56 Evička 31 108 tomi 28 110 Ján Machník 23 77 Stefan Galdik 14 41 Marek Tobias 13,5 44 Martin Rexa 6 35 Adrián Struhár 0 58
Trochu iný šach – Prológ
Trochu iný šach – Lekcia 1
Trochu iný šach – Lekcia 2 Dvojťažky
Trochu iný šach – Lekcia 3 Trojťažky
[feather_follow]