Trochu iný šach – Lekcia 7 Pomocné maty

Riešenia úloh z predchádzajúcej lekcie

 

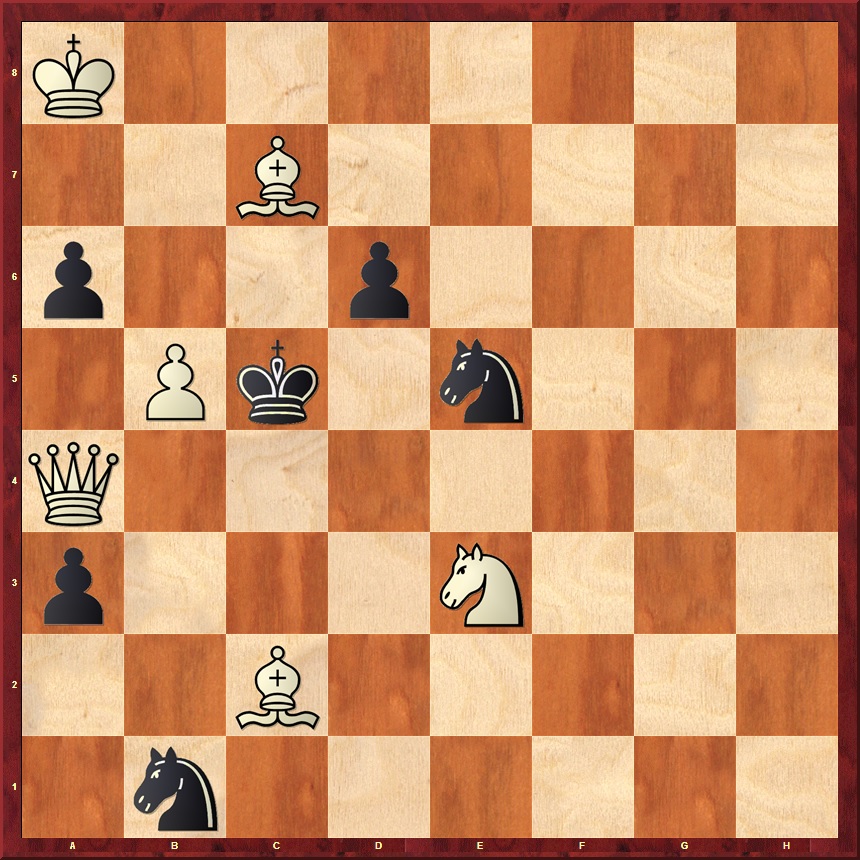	J. Pospíšil, Humoristické listy 1887 1. Sd8 (2. Kb7) (1.2) 1… Jd2 2. Da3 (1.2) 1… Jc3 2. Dd4+ (1.2) 1… axb5 2. Da7+ (1.2) 1… d5 2. Se7+ (1.2)
	V. Sichev, Memoriál Nabokova 1994 1. Jbd2 (2. Vxe4+) (1.2) 1… Vxd2 2. Va8 (1.2) 1… Vc3 2. Vd5 (1.2) 1… Sc3 2. Jc4 (1.2) 1… e3 2. Vaxe3 (1.2) 1… d3 2. Vxe4+
	Ernest Pogosianc, Ja tvoriu po vdochnoveniu 2001 1. Se4 (1) Vg8 2. Sf5+ Kh4 3. Sc8 (1) Vg1 4. Se6 (3) Va1+ 5. Sa2 (2) Vxa2+ 6. Kb3 Va1 7. Kc2 (2) Va2+ 8. Kc3 Va3+ 9. Kc4 Va4+ 10. Kxc5 Va5+ 11. Kc4 Va4+ 12. Kc3/Kb3 Va3+/Va1 13. Kb2 (1)
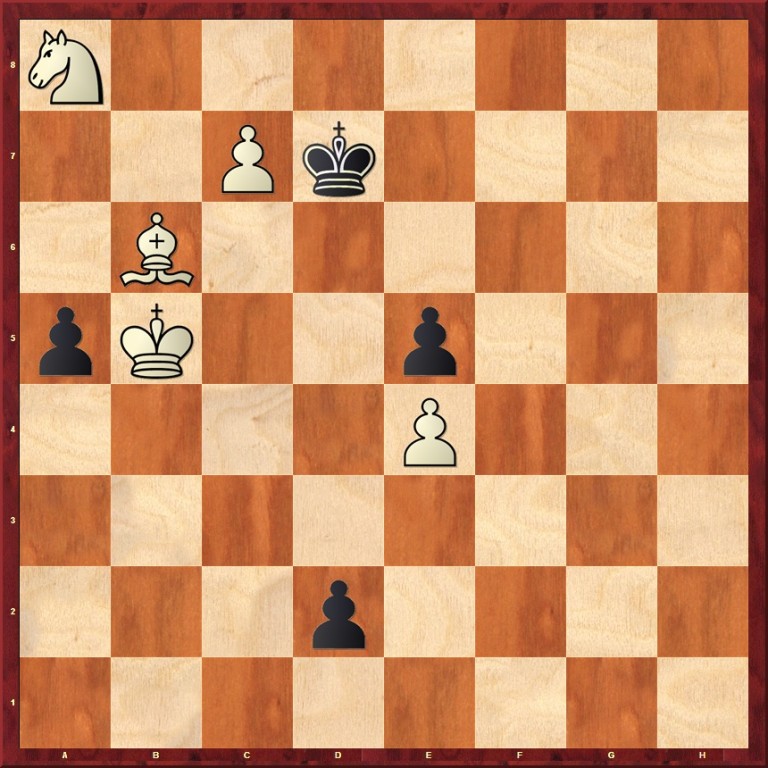	E. Bachrameev a S. Maksimov, Gorkovskaja pravda, 1981 1. Ka6 (2) Kc8 2. Sa7 d1D 3. Sb8 (2) Dd3+ 4. Ka7 Dd4+ 5. Jb6 (2) Dxb6+ 6. Kxb6 a4 7. Ka7 a3 8. Ka8 a2 9. Sa7 (4) a1D pat Vedľajšie riešenie: 1. Sa7 d1D 2. Ka6 Dd3+ 3. Kb7 Dxe4+ 4. Kb8 Dxa8+ 5. Kxa8 Kc8 6. Se3! 6. Sc5? Kxc7 7. Ka7 Kc6 8. Sa3 Kb5 9. Kb7 e4 10. Sc1 a4 11. Kc7 Kb4 12. Kd6 a3 13. Kd5 a2 14. Sb2 e3 0-1
	W. A. Bron, Tornooi nationaal comité L.O en Sport, 1957 1. Ve4+ Kd3 2. Sc4+ Kxd2 3. Ve2+ Kd1/Kc3 4. Vxc2 (2) Kxc2 5. b7 (2) Se7 6. Sd3+ (4) Kxd3 7.b8D Sd6+ 8. Kg5 Vg6+ 9. Kf5 (2) Sxb8 pat

Hodnotenie kongresu

Ako som sľuboval v predchádzajúcej lekcii, na úvod krátka správa zo Svetového kongresu kompozičného šachu, ktorý sa odohral 30.7-6.8 v Belehrade v Srbsku. Súťaží, najmä skladateľských, sa uskutočnilo ozaj neúrekom (vyhodnotenie všetkých trvalo spolu takmer 5 hodín a bolo rozdelené na niekoľko častí!), takže sa obmedzím iba na riešenie. Podrobné informácie a výsledky všetkých súťaží možno nájsť na kongresovej stránke.

Majstrovstiev sveta v riešení sa zúčastnilo 89 riešiteľov z viac ako 20 krajín sveta. Dominantnú pozíciu na riešiteľskej scéne už tradične potvrdilo Poľsko, ktoré suverénne zvíťazilo v kategórii družstiev a jeho dvaja najlepší riešitelia Kacper Piorun a Piotr Murdzia obsadili so zhodným počtom 83,8 bodov z 90 a bezpečným náskokom 1. a 2. a druhé miesto v súťaži jednotlivcov. Majstrom sveta pre rok 2016 sa stal Kacper Piorun, na druhom mieste teda skončil už spomínaný Piotr Murdzia a tretí sa umiestnil domáci organizátor Marjan Kovačević. Aj vďaka skvelému výkonu Kovačevića získal tím Srbska bronzovú medailu, čo na druhej strane nie je až také nečakané, kedže ide o tím zložený výhradne z veľmajstrov. Prekvapením a veľkou senzáciou však bolo umiestnenie Litvy na striebornej pozícii. Litva má dvoch silných mladých riešiteľov Vidmantasa Satkusa a Martynasa Limontasa, ktorí v posledných rokoch stabilne získavajú na výkonnosti a ich postup, v spojení s dobrou tímovou súhrou, keď si títo dvaja vykrývali bodové straty s tretím členom tímu Vilimantasom Satkusom (v každom kole sa počítajú body dvoch najlepších), bol teraz korunovaný skvelým umiestnením.

Slovenská reprezentácia po napínavom závere nakoniec ostala tesne pred bránami prvej desiatky na 11 mieste. Spomedzi slovenských riešiteľov najvyššie skončil IM Tomáš Peitl (68,5b, 20. miesto), avšak ani on, ani FM Marek Kolčák (51b, 66. miesto) nedokázali získať počet bodov zodpovedajúci ich ratingu a domov si odviezli ratingovú stratu. Naproti tomu, tretí člen tímu FM Vasil Ďačuk (63,5b, 41. miesto) sa umiestnil nad papierové očakávania a domov si odváža ratingový zisk. Vasil za Slovensko štartoval premiérovo, keďže pochádza z Ukrajiny a tento rok získal slovenské občianstvo. Je to vynikajúci riešiteľ, sme veľmi radi, že ho môžeme mať v tíme a dúfame, že v ďalších súťažiach nám táto posila pomôže pomýšľať na medajlové umiestnenie. Na majstrovstvách sveta vo farbách Slovenska štartovali ešte Juraj Lörinc (46,4b, 72. miesto) ako jednotlivec a Oliver Ralík (15b, 88. miesto) ako senior, ich výsledky sa však nepočítali do výsledkov tímu.

V sprievodnom OPENE súťažili 119ti riešitelia, zvíťazil majster sveta Kacper Piorun (48/60b) pred domácim Vladimirom Podinićom (41,6b) a Oferom Comayom (39,1b) z Izraela. Slovenskí riešitelia sa zúčastnili v rovnakej zostave ako na majstrovstvách sveta, avšak jediný, ktorý dosiahol výsledok lepší, ako papierové očakávania, bol Oliver Ralík, ktorý skončil s 15,5 bodmi na 92. mieste a pripísal si vyše 20 bodov ratingu. Úlohy v OPENE boli mimoriadne náročné, ako ukazuje aj relatívne nízky bodový zisk prvých troch umiestnených. V Solving Show – zábavnej súťaži v rýchlom riešení dvojťažiek – sa nečakane darilo Tomášovi Peitlovi, ktorý získal striebornú medailu po tom, ako podľahol vo finále azerbajdžánskemu juniorovi Zaurovi Mammadovovi. Na treťom mieste skončil veľmajster Jonathan Mestel z Veľkej Británie.

Srbskí organizátori priniesli množstvo moderných prvkov do viac-menej zabehaného systému organizácie kongresu. Aj keď to možno nie vždy vyšlo ideálne, patrí im veľká vďaka za inovatívny prístup, vydláždenie cesty pre budúcich organizátorov a, samozrejme, za príjemný týžďeň strávený v srbskom hlavnom meste.

Pomocné maty

Po tomto úvode sa dostávame k samotnej lekcii. Letné prázdniny síce ešte doznievajú, avšak my sa hneď priam hlavou vpred vrháme do úplne neznámych vôd pomocných matov. Úlohy, ktoré sme riešili doteraz možno boli zvláštne, ale bol to stále šach, ako ho poznáme. Niektoré, najmä štúdie, by sa možno dali považovať aj za užitočné v praktickej partii. Dobre to vystihuje práve názov nášho seriálu – bol to taký trochu iný šach.

Odteraz to bude úplne iný šach. V pomocných matoch (hovorovo pomocníkoch) totiž, ako naznačuje už názov, biely a čierny nesúperia v boji o to, kto dá druhému mat, práve naopak – pomáhajú si s cieľom dať mat čiernemu. Ak by sme to chceli povedať formálne, napríklad klasická dvojťažka znamená, že „existuje ťah bieleho taký, že na každý ťah čierneho, existuje ťah bieleho taký, že je mat“. Pomocný mat druhým ťahom (zvyčajne nehovoríme „pomocná dvojťažka“) znamená, že „existuje ťah čierneho taký, že existuje ťah bieleho taký, že existuje ťah čierneho taký, že existuje ťah bieleho taký, že je mat“. Toto je veľmi zvláštne, vysvetlíme si to poriadne.

Pomocný mat n-tým ťahom (druhým, tretím, atď) je taká úloha, v ktorej začína čierny a riešenie je legálna postupnosť šachových ťahov striedavo čierneho a bieleho (ako v normálnom šachu), ktorá končí matujúcim ťahom bieleho, pričom každá zo strán urobí nanajvýš n ťahov. Pomocný mat n,5-tým ťahom (dva-a-poltým, tri-a-poltým, atď) je taká úloha, v ktorej začína biely a riešenie je legálna postupnosť šachových ťahov striedavo čierneho a bieleho (ako v normálnom šachu), ktorá končí matujúcim ťahom bieleho, pričom čierny urobí nanajvýš n ťahov a biely urobí nanajvýš n+1 ťahov. Pomocný mat n,5-tým ťahom je teda ako pomocný mat n+1-vým ťahom, ale prvý ťah čierneho je vynechaný. Pomocné maty označujeme h#n, prípadne h#n,5, teda napríklad h#2 alebo h#3,5 (h z anglického helpmate).

V predchádzajúcom odstavci používame výraz „legálna postupnosť“, čo sa tým ale myslí? Myslí sa tým to, že všetko je v súlade s pravidlami šachu. Teda, pokiaľ má napríklad jedna zo strán šach, musí sa mu ubrániť a podobne. Jediný rozdiel oproti klasickému šachu je teda to, že biely a čierny spolupracujú aby dali mat čiernemu – pravidlá sa inak nijako nemenia. Dá sa to predstaviť aj tak, že pomocný mat je niečo, čo by mohli súperi urobiť v partii, ak by chceli zabezpečiť, aby jeden z nich vyhral – spolupracovali by, ale stále by museli hrať podľa pravidiel, aby partia dávala zmysel.

Pomocné maty majú často viac ako jedno riešenie. V skutočnosti, pomocný mat, ktorý ma iba jedno riešenie je veľkou raritou (pokiaľ nemá veľmi veľa ťahov, teda viac ako 6) a skladateľ musí mať veľmi dobrý dôvod, aby taký zložil – musí to byť veľmi pekný motív, ktorý sa jednoducho nedá spracovať vo viacerých riešeniach. Zároveň, pre pomocné maty platia absolútne najprísnejšie estetické pravidlá zo všetkých druhov úloh. V praxi to znamená, že riešenia musia mať presnú dĺžku (žiadne krátke riešenia) a pravidlo ekonómie je povýšené tak, že v každom riešení musia byť zapojené všetky biele figúry (alebo byť brané). Riešenia by taktiež mali byť spojené nejakou analógiou, motívom, ktorý sa opakuje vo viacerých z nich – táto analógia tvorí hlavný estetický obsah úlohy. Nesmú byť ale príliš podobné – teda napríklad začínať rovnakým ťahom. Ukážeme si to na príklade.

Poznámka: riešenia všetkých ilustračných príkladov sú zhrnuté na konci lekcie.

Fadil Abdurahmanovic, Mat, 1980, h#2, 2 riešenia

Pozícia je už od pohľadu veľmi zvláštna. To preto, že v pomocných matoch sa neberie ohľad na také maličkosti, ako či sa figúry napádajú alebo či hrozí bielemu brutálny šach, prípadne rovno mat, pretože je to jedno. Súperi spolupracjú, takže aj pozícia, v ktorej sa navzájom napádajú nekryté dámy dáva zmysel. Zároveň vidíme, že je pripravená analógia batériovej hry na stĺpci a diagonále. Nezabúdajme, že stále platí, že hľadáme pekné a nečakané ťahy. A čo je krajšie a nečakanejšie, ako keď čierny v prvom ťahu so šachom vezme bielemu dámu? Po braní dámy sa uvoľnuje pre čierneho kráľa prístup na pole d4, kam môže ísť v druhom ťahu. Ako mu ale dať potom mat? Môžeme si všimnúť, že keby strelec „nezavadzal“ na c4, mohli by sme dať mat Vc4. V kombinácii s tým, že Sg8 môže prekryť úvodný šach a dokonca sám dáva odkrytý šach, je zrazu všetko jasné: riešenie je 1. Dxh8+ Sg8+ 2. Kxd4 Vc4#. Úloha však ešte nie je vyriešená. Ostáva nájsť druhé riešenie, ktoré je ale veľmi analogické a nemalo by nám robiť problém. Táto úloha je vskutku nádherná, pretože dochádza k plnej analógii vo všetkých ťahoch – v prvom ťahu čierny so šachom berie figúru bieleho, ktorá kryla pole pri čiernom kráľovi, biely predkrýva figúrou, ktorá odchádza z poľa, na ktorom bude matovať a dáva odkrytý šach, čierny ide na uvoľnené pole a berie ďalšiu figúru a biely matuje na poli, ktoré si uvoľnil v prvom ťahu.

Všimnite si, že v pomocných matoch píšeme najprv ťah čierneho, až potom ťah bieleho, nezačíname teda 1… Dxh8+. Takto zápis skončí elegantne, 2. ťahom bieleho. Zároveň je treba riešenie napísať až do konca, teda až do matujúceho ťahu. Čiastočné riešenia nezískavajú čiastočné body, avšak ak má úloha viacero riešení a nájdete iba niektoré z nich, dostanete čiastočný počet bodov. Maximálny počet bodov za pomocný mat bude v našej súťaži 12 bodov.

Predtým, ako začneme skúmať spôsoby riešenia pomocných matov, pozrime sa ešte na príklad pomocného matu, v ktorom začína biely. Takéto úlohy sa vyskytujú relatívne zriedka, ale predsa ich uvádzame pre úplny obraz.

Hans Peter Rehm, Feenschach 1998, 2. čestné uznanie, h#4,5

Úloha ma iba jedno riešenie, čo signalizuje, že bude náročná, pretože sa nemôžeme spoliehať na analógie. Môžeme si všimnúť, že čierny kráľ je relatívne voľný, ale keby sme ho presunuli na e4, bol by hneď v obkľúčení a navyše by mu hrozil potenciálny mat pešiakom na d3. Strelec by sa mohol uhnúť na d5, jazdec zapchá f5 a čiernopolný strelec by sa mohol predkryť na e3, aby zabránil pôsobnosti veže a zapchal aj toto pole. Problémom však ostáva, ako vyriešiť odťažný šach po Jf5 (biely kráľ nemá kam ustúpiť) a práve na to musíme využiť bieleho strelca. Čitateľ už istotne príde na to, ako to urobiť.

Ako riešiť pomocné maty

V tejto chvíli sme si už dostatočne ujasnili, čo je to ten pomocný mat, nastáva teda otázka, ako ich riešiť? Prirodzená možnosť je skúšať všetky možné kombinácie ťahov, ale to sa ukazuje ako veľmi neefektívne jednak preto, že ich je príliš veľa a tiež preto, že človek si, zdá sa, nevie poriadne zapamätať, čo už skúšal a čo ešte nie a po čase začne chodiť v kruhu. Potrebujeme preto lepšiu metódu.

Pomocné maty sa vyznačujú tým, že biely má zvyčajne veľmi málo figúr, často len jedinú okrem kráľa. Dobrý spôsob je preto pokúsiť sa identifikovať všetky možné matové obrazce, ktoré by prichádzali do úvahy. Pod matovými obrazcami rozumieme pozície (alebo skôr útržky pozícií), v ktorých je čierny kráľ v mate. To znamená, že vyberieme pole, na ktorom čierny kráľ dostane mat, konšteláciu bielych kameňov a doplníme čiernymi blokujúcimi kameňmi. Pokiaľ má biely málo materiálu, často prichádza do úvahy iba niekoľko matových konštrukcií. Dobrý spôsob je tiež skúmať, či nie sú niekde podozrivo nakopené čierne figúry, aby vo svojom strede umožnili dať čiernemu kráľovi mat.

Keď si už vyberieme nejaký matový obrazec, potrebujeme vyhodnotiť, či je možné ho v danom počte ťahov dosiahnúť. Na toto potrebujeme spočítať, koľko ťahov potrebuje čierny kráľ, aby prišiel na pole matu, koľko ťahov potrebujú biele figúry, aby sa k nemu dostali a koľko polí okolo neho dokážu pokryť a nakoniec, koľko ťahov potrebujú zvyšné čierne figúry, aby pokryli zvyšné polia. Ak nám tieto počty sedia, môžeme začať skúšať, či vieme nastaviť poradie ťahov figúr tak, aby všetko vyšlo – teda či si niektoré líniové figúry nezavadzajú pri presune alebo či nedávajú cestou nejaké nežiadúce šachy, ktoré znemožňujú zamýšľané poradie ťahov. Pri skúšaní je dôležité zistiť, či sa nevyskytujú nejaké ťahy, ktoré možno spraviť v rôznych verziách. Myslím tým napríklad to, že pokiaľ nejaká čierna figúra iba ustupuje, aby nezavadzala a môže ústupiť na 2 alebo viac polí bez toho, aby v tom bol nejaký podstatný rozdiel, zrejme sme na zlej stope, pretože ťahy musia byť jednoznačné.

Malou osobitnou podkategóriou v rámci pomocných matov sú dvojťahové pomocné maty, v ktorých má biely zvyčajne trochu viac materiálu (oproti dlhším pomocníkom). V týchto úlohách je najlepšie spoliehať sa na analógiu medzi riešeniami, pričom veľa napovie niekedy už aj počet riešení. Analógie však určite treba hľadať aj pri dlhších úlohách.

Tieto pravidlá sú veľmi teoretické a takto na prvý pohľad sa môžu zdať nezrozumiteľné, prejdeme preto bez zbytočných prieťahov rovno k príkladom, na ktorých si ich ilustrujeme.

Fadil Abdurahmanovic, Mat, 1980, h#2, 2 riešenia

Biely má celkom dosť figúr, ktoré sú navyše roztrúsené a ak chceme zabezpečiť, aby hrali v riešení, budeme ich musieť rýchlo skoordinovať. Pozornosť upúta dvojica čiernych jazdcov, ktorí by mohli odskakovať a tak rozohrať bielu vežu na b4. Ak však odskočia obaja, nevidno veľmi, ako by biely mohol matovať. Mohol by však odskočiť vždy len jeden – tu zbystríme pozornosť, pretože riešenia sú práve dve, takže by to pekne vychádzalo – a veža z b4 by mohla plniť väzobnú funkciu. Skutočne, jazdec z c4 by mohol ísť na e5 a uvoľniť tak cestu kráľovi na f4. Treba však ešte nájsť mat. Vidíme, že po Je5 a Kf4 sú obaja jazdci vo väzbe a spoločne kryjú pole f3. Aké by to bolo pekné, keby práve na tom poli vychádzal mat a veruže tam aj mieri dáma, ale kryje ho ešte pešiak z g4. Jedine, že by sme aj jeho dali do väzby… Druhé riešenie nájdeme opäť čisto pomocou analógie a nechávam to znovu na čitateľa.

V predchádzajúcom príklade sme neuplatnili princíp hľadania matových obrazcov, pretože sa úlohu podarilo vyriešiť aj bez neho. Ak by sme ho však predsa len chceli použiť, mohli by sme uvažovať nasledovne. Čierny kráľ je voľný a za dva ťahy k nemu nestíha prísť dostatok blokujúcich kameňov. Na e4 a najmä na f4 by bol však oveľa viac stiesnený – kamene na f5, g5 a g4 sú veľmi podozrivo rozostavené. Zároveň, ak chceme kráľa dostať na f4, musí mu buď biely uhnúť, na to ale nie je čas, alebo si musí čierny pomôcť sám – prekrytím.

Fadil Abdurahmanovic, The Problemist, 1987, h#2, 3 riešenia

K tejto krásnej úlohe môžeme istotne pristupovať viacerými spôsobmi, môj myšlienkový pochod bol takýto. Samozrejme, najradšej by som dal mat dvojšachom, ale zdá sa, že nepôjde pokryť ani d7 ani f7, aby sa to dalo urobiť. Navyše, úloha má tri riešenia a toto by nemalo žiadne analógie. Podozrivá je však piata rada, na ktorej stojí biely kráľ a 3 ťažké figúry. Vyzerá to tak, že hra sa bude odohrávať na tejto línii a čierna dáma má dokonca práve 3 ťahy po nej, ktoré nič neberú. Žeby náhoda? Estetika každopádne káže vyskúšať, a keď už čierna dáma ide jedným smerom, biela by ju mohla nasledovať, koľko sa len dá – toto je jeden zo všeobecných motívov kompozičného šachu. Takto sa nám črtajú tri riešenia začínajúce 1. Dg5 Df5+, 1. Df5 De5+, 1. De5 Dd5+ a čitateľ si už iste ľahko overí, ako sa tieto úvody dajú doplniť na celé riešenia.

Moje riešenie sa do veľkej miery odvíjalo od nepriamych indícií, ako je počet riešení, či istá estetika. Chcem ale podotknúť, že sa dá naň prísť aj ináč, možno systematickejšie. Totiž, keď si uvedomíme, že čierny kráľ ma príliš voľného miesta na e6, je len prirodzené, pokúsiť sa ho dostať do matovej siete na piatej rade. O to viac, keď si všimneme, že má k dispozícii práve 3 polia – d5, e5, f5 – jedno na každé riešenie. Demonštruje sa tu však opakovane aj to, že už len samotný počet riešení môže byť veľkou pomôckou.

G. Paros, h#3, 1 riešenie

Úloha s jedným riešením znamená, že to asi bude niečo veľmi pekné, ale zároveň nečakané. Skúsme si najprv určiť, kde a ako budeme matovať čierneho kráľa. Na a5 sa zdá byť veľmi ďaleko, ale také b6 aj c7 vyzerajú sľubne. Na b6 by mohol mat vzniknúť napríklad po čiernych ťahoch Sa7, Kb6 a a5 dámou z d6, ale na to by biely musel odstrániť čiernu vežu z h6 a to sa už nestíha. Iné obrazce na b6 veľmi nevychádzajú, takže ostáva skúsiť c7. Čierny potrebuje 2 ťahy len aby sa tam dostal, takže mu ostáva jediný aby nejako bielemu umožnil dať mat. Ak by biely matoval z d8, čierny by musel nejako zahatiť cestu dáme a ešte odísť strelcom z c8, aby dáma kryla aj b8 a to jedným ťahom nestíha, mat z d8 teda zavrhujeme. Ostáva matovanie z e5 s tým, že biely by mohol pokryť b6 pešiakom z a5 a čierny by sa mohol postarať o to, aby veža z h6 nezavadzala. Ak ale čierny ustúpi Vh5, biely musí brať na g7 aby dostal dámu do kontaktu s poľom e5, čím ale znemožňuje čiernemu kráľovi príchod na c7. Druhá možnosť, ako môže čierny zrušiť pôsobnosť svojej veže je prekrytím g6 a biely sa potom ocitá v pozícii, keď musí urobiť vyčkávací ťah. Dáma má k dispozícii celú diagonálu, ale čitateľ už isto overí, že správne je iba jediné pole.

Úlohy, ktoré sme videli doteraz boli síce veľmi pekné, ale neboli to úplne typické príklady takých, s ktorými sa stretnete na súťažiach. Najštandardnejšie zloženie kola pomocných matov je dvojťahový pomocník s 3 až 4 riešeniami, trojťahový pomocník s 2 alebo 3 riešeniami a päťťahový pomocník s 2 riešeniami. Je to takým nepísaným pravidlom a na majstrovstvách sveta a Európy sa ho väčšinou rozhodca snaží dodržať. Pozrime sa teda, ako takéto typické úlohy vyzerajú.

Josef Kupper, The Problemist, 2002, h#2, 3 riešenia

Jedna z klasických figúrových kombinácií – dvaja strelci a veža. Na riešenie takýchto úloh treba mať nacvičené matové obrazce s dostupným bielym materiálom a táto úloha krásne ukazuje 3 možno až najtypickejšie. Prvý z nich je veža stojaca za kráľom diagonálne a strelec matujúci po tejto diagonále a vzniká po ťahoch bieleho Vg3 a Sb8, druhý je strelec stojaci za kráľom ortogonálne (po stĺpci alebo riadku) a veža matujúca po tejto línii a vzniká po ťahoch bieleho Se4 a Vg4 a tretí sú takzvaní „Horwitzovi strelci“, ktorých poznáme aj z klasického šachu, teda dvaja strelci na dvoch susedných diagonálach, z ktorých jeden matuje. Tento motív vzniká v našom prípade po ťahoch bieleho Sg6 a Se3 a je v našom prípade trochu pozmenený, pretože jeden zo strelcov stojí priamo pri čiernom kráľovi, a tým zapája aj vežu, ktorá ho kryje. S týmito informáciami už čitateľ úlohu istotne vyrieši.

Tiež chcem upozorniť na obsah a analógiu v úlohe – jedná sa o cyklus dvojíc figúr, z ktorých jedna ťahá v prvom ťahu a druhá matuje a tieto dvojice sú v každom riešení iné. Analógia je tu však jemne poškodená, pretože bielopolný strelec ani raz nematuje, za to čiernopoľný matuje dvakrát (bezchybné by to bolo, keby každá figura raz ťahala v prvom ťahu, raz matovala a raz stála na mieste – tri figúry, tri role, tri riešenia). Je to veľmi dobrý príklad súťažnej úlohy, ktorá má síce veľa analógie, ale nedá sa spoľahnúť úplne na všetko.

Christopher Feather, nepublikovaná, h#3, dvojník Vh8 -> a8

Jeden koncept, o ktorom sme doposiaľ nehovorili je takzvaný dvojník. Normálne je cieľom skladateľa vytvoriť úlohu, ktorá má viacero analogických riešení, avšak nie vždy sa to podarí, a vtedy môže situáciu zachrániť práve dvojník. Dvojník je taká úloha, ktorá sa od pôvodnej líši iba veľmi málo, presunom jednej figúry či pešiaka, alebo iba odobratím alebo pridaním kameňa. Dvojník je teda takmer na nerozoznanie od pôvodnej úlohy a z toho dôvodu sa považuje za povolenú súčasť úlohy. Ak riešime úlohu s dvojníkom, riešime vlastne 2 rôzne úlohy (alebo aj viac, ak je dvojníkov viac) a je veľmi dôležité správne si vybrať, ktorou začneme, pretože obtiažnosť sa môže veľmi líšiť a analógia nám môže pomôcť nájsť ďalšie riešenia, ak už máme jedno. Často to býva tak, že autor vyberie ako hlavnú pozíciu tú, ktorá sa mu zdá náročnejšia, teda sa zvyčajne oplatí začať B pozíciou (A pozícia je základna a dvojníky sa označujú ďalšími písmenami B, C, atď).

Úloha v našom príklade je mimoriadne náročná a nemá nejakú extra peknú analógiu, takže bez nejakého rozsiahlejšieho komentára uvádzam priamo riešenie. Aby sme ho našli, musíme jednoducho skúšať matové obrazce, so samotným jazdcom a na kraji šachovnice ich nie je až tak veľa. Riešenie: A: 1. Kf8 Ke5 2. De8 Jf6 3. Vg8 Jh7# B: 1. 0-0-0 Kxf7 2. Kd7 Kxg7 3. Ke8 Jf6#.

Tivadar Kardos, Comm., Magyar Sakkelet, 1976, h#5, 2 riešenia

Na záver lekcie uvádzame príklad takzvaného dlhého pomocného matu – teda takého, čo má viac ako 4 ťahy. Pri dlhých samomatoch si musíme ako úplne prvé overiť, či môže dôjsť k nejakým premenám na jednej či druhej strane a ak áno preskúmať, či sa tak nedá náhodou dať mat. Premeny totiž dodávajú veľký potenciál, ktorý je na začiatku v pozícii skrytý – ťažko môžeme hľadať matové obrazce, keď nevieme ani, aký bude na konci materiál. V našom príklade si môžeme všimnúť, že biely h-pešiak stíha za 5 ťahov dôjsť až na h8 a premeniť sa, ale už nebude mať žiaden ďalší ťah, takže jednak mu musí niekto odstrániť z cesty vežu z h6 a tiež po premene na h8 musí byť priamo mat. To by sa dalo docieliť tak, že čierny kráľ by bol na f8 a veža by blokovala pole e7 a naozaj, čierny kráľ sa na 4 ťahy vie dostať na f8 a ešte aj cestou zobrať bielu vežu – prvé riešenie je hotové.

Ešte sme neoverili možnosti čiernej premeny. D-, či f-pešiaci sa premieňať nebudú, síce by to stihli, ale nič by z toho nebolo a čierny kráľ by ostal na voľnom priestranstve. Premieňať by sa teoreticky mohol a-pešiak, ale museli by sme vyslobodiť bieleho kráľa braním Vxb2. Vyslobodený biely kráľ by potom mohol postupovať bližšie k čiernemu kráľovi, aby uzavrel matovú sieť, zatiaľ čo premenená čierna figúra by sa priblížila k čiernemu kráľovi a zablokovala niektoré pole. Otázkou pre čitateľa ostáva, či a ako sa to dá urobiť tak, aby všetko vyšlo. Pomôcka – spočítajte si, koľko najviac polí dokáže pokryť biely okolo čierneho kráľa a či po celom vyslobodzovacom manévri ešte ostane čiernemu čas na ťahy kráľom.

Videli sme niekoľko relatívne rôznych druhov pomocných matov. Pravdou je, že je to len špička ľadovca, no táto lekcia je už beztak dosť dlhá. V pomocných matoch ešte viac ako v ostatných oddeleniach platí, že treba veľa riešiť. Iba tak sa človek totiž naučí to množstvo štandardných konštrukcií a matových obrazcov, ktoré sa v pomocných matoch používajú a ľahšie bude vedieť, na čo sa má v úlohe zamerať. Pomocné maty sú totiž v konečnom dôsledku vždy o tom istom – zistiť kde a ako sa bude dávať mat a potom nájsť spôsob ako vyskladať ťahy v správnom poradí. Treba sa teda naučiť rôzne matové obrazce, ktoré sa vyskytujú a rôzne zvraty, ktoré sa používajú na určenie poradia ťahov – teda na zdôvodnenie, prečo nie je možné ťahy vykonať v inom poradí. Toto pravidlo je treba mať vždy na pamäti – ak sa nám zdá, že v niektorej línii uvažovania sa budú vyskytovať nerozlíšiteľné ťahy, alebo ťahy, ktorých poradie je zameniteľné, je to jednoznačný dôkaz, že sme na zlej stope.

Myslím si však zároveň, že pomocné maty, keď si na ne človek už trochu zvykne, sú veľmi zábavné a ich riešenie spôsobuje veľkú radosť. Čo sa týka mňa osobne, je to jednoznačne moje najobľúbenejšie oddelenie, takže dúfam, že aj vám pomocné maty učarujú.

Riešenia príkladov

Príklad 1: 1. Dxc8+ Vd8+ 2. Kxc4 Dd4#.

Príklad 2: 1… Sb8 2. Sd5 Sd6 3. Ke4 Sc5 4. Jf5+ Se3 5. Sxe3 d3#. Opäť upozorňujem na paradoxný zápis – začína biely, ale v zápise je 1… Sb8 z už spomínaných dôvodov.

Príklad 3: 1. Je5 Vh4 2. Kf4 Df3#; 1. Jf3 Dh7 2. Ke4 Ve8#.

Príklad 4: 1. Dg5 Df5+ 2. Kxf5 Jg3#; 1. Df5 De5+ 2. Kxe5 Jc3#; 1. De5 Dd5+ 2. Kxd5 Jf4#

Príklad 5: 1. g6 Da1 2. Kb6 a5+ 3. Kc7 De5#

Príklad 6: 1. Je7 Vg3 2. Jg8 Sxb8#; 1. Jc3 Se4 2. De5 Vg4#; 1. Jc7 Sg6 2. Kg5 Se3#. Dodatočne ešte analógie v prvom ťahu čierneho!

Príklad 8: 1. Kg5 h4+ 2. Kxh6 h5 3. Kg7 h6+ 4. Kf8 h7 5. Ve7 h8D#; 1. Ve2 h4 2. Vxb2 Kxb2 3. a1V Kc3 4. Vg1 Kd4 5. Vg4 Vxf6#

Úlohy n,5-tým ťahom nebudem dávať a obe strany urobia n legálnych ťahov a čierny musí skončiť v mate. Čiastočné riešenia sa nebodujú, bodujú sa správne riešenia a celkový bodový zisk závisí od počtu správnych riešení.

Súťažná úloha č. 26

h#2, 2 riešenia
ČNT Úloha za 12 bodov

Súťažná úloha č. 27

h#2, 4 riešenia
ČNT Úloha za 12 bodov

Súťažná úloha č. 28

h#3, 2 riešenia
ČNT Úloha za 12 bodov

Súťažná úloha č. 29

h#4, dvojník: čierny Jd7 sa presúva na d8
ČNT Úloha za 12 bodov

Riešenia z Lekcie 7 poslané do 2.10.2016 23:59 budú započítané do súťaže.

Riešenie pošli formulárom nižšie. Nezabudni napísať číslo súťažnej úlohy.

[contact-form-7 id=“4084″ title=“Kompozičný šach“]
Tréningové šachové DVD

Priebežné poradie po Lekcii č.6
#	      Nick	                 Počet bodov	   PH1
1	Jozef	             146	77
2	Bohuslav Czudek	     146	130
3	janjurco 	     139	125
4	OndrejFranko	     129	72
5	Peter Lukáč	     102.2	185
6	PaeDr. Ján Husák     84.4	86
7	Ján Machník	     59.8	167
8	Milan Svrček	      43	108
9	tomi	              41	160
10	Evička	              31	108
11	Stefan Galdik 	      14	41
12	Marek Tobias	     13.5	44
13	Martin Rexa	       6	35
14	Adrián Struhár	       2	81

Partneri súťaže

  

Trochu iný šach – Prológ
Trochu iný šach – Lekcia 1
Trochu iný šach – Lekcia 2 Dvojťažky
Trochu iný šach – Lekcia 3 Trojťažky
Trochu iný šach – Lekcia 4 Štúdie
Trochu iný šach – Lekcia 5 Zo života
Trochu iný šach – Lekcia 6 Svetový kongres

[feather_follow]