Trochu iný šach – Lekcia 8 Mnohoťažky

Komentár k riešeniam predminulej lekcie

Pri úlohe č. 24 som uviedol riešenie začínajúce ťahom 1. Sa7 ako chybné aj s príslušným vyvrátením. Ako však správne poukázali niektorí riešitelia, chybné je akurát toto „vyvrátenie“ a 1. Sa7 skutočne vedie k remíze. Kľúčovou chybou vo vyvrátení je ťah 6. Sc5??, po ktorom biely naozaj prehráva. Namiesto toho, ako jediné udržuje remízu 6. Se3, ktoré nevedie k strate tempa po ťahu Kc6. Rozhodol som sa teda udeliť body aj riešiteľom, ktorí uviedli toto vedľajšie riešenie.

Riešenia úloh z predchádzajúcej lekcie

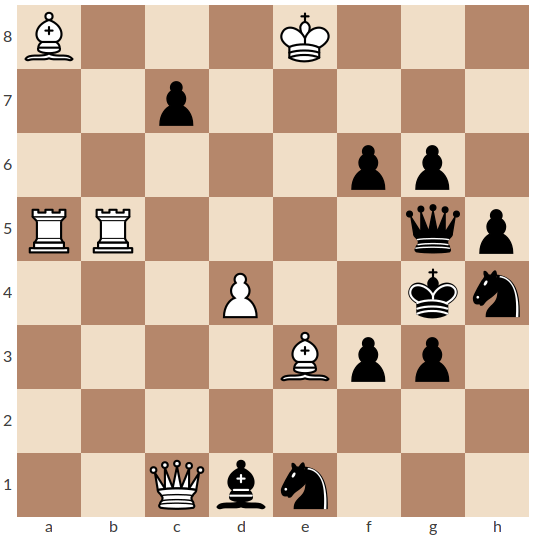	F. Abdurahmanovic, Shahmatna misl, 1982, 1. cena 1. Dxb5+ Dc6 2. Kf5 Dd7# (6) 1. Dxe3+ Ve5 2. Kf4 Ve4# (6)
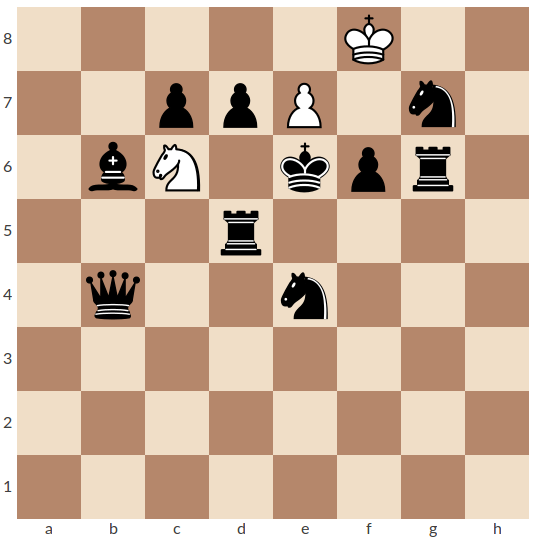	H. Rehm, MK Segal 1962, 1. cena 1. Kd6 e8D 2. dxc6 De7# (3) 1. d6 e8V+ 2. Kd7 Jb8# (3) 1. Vd6 e8S 2. Jf5 Sf7# (3) 1. Jd6 e8J 2. Vh6 Jxg7# (3)
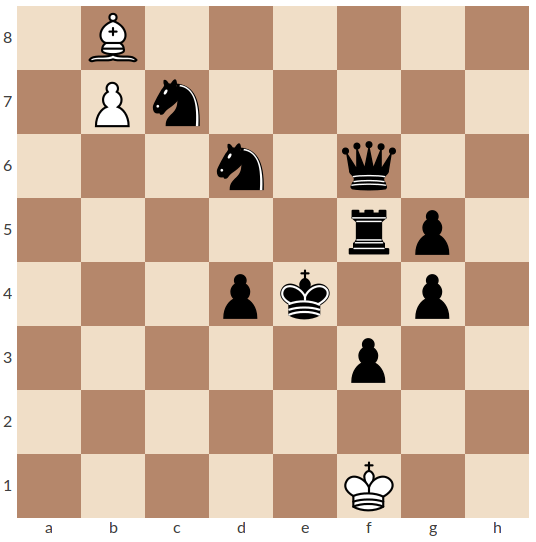	T. Garai, originál pre Šachové umění 2002 1. Ja8 bxa8J 2. Kf4 Jc7 3. Je4 Jd5# (6) 1. Jc8 bxc8V 2. Jd5 Vc7 3. Ke5 Ve7# (6)
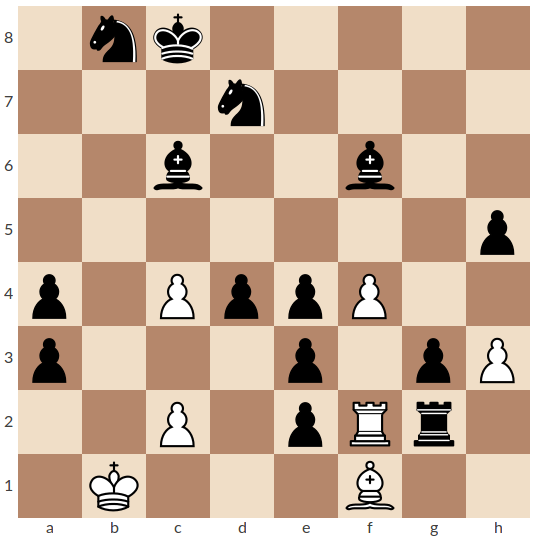	Gennady Kozyura & Yuri Gordian, The Problemist, 2002 A: 1. Sd5 cxd5 2. e1J Sc4 3. Jxc2 Vxc2 4. Sd8 Sa6# (6) B: 1. Sg5 fxg5 2. Vh2 Vf5 3. Vxh3 Sxh3 4. Sb7 Vc5# (6)

Mnohoťažky

Po vcelku exotickej lekcii pomocných matov sa vraciame naspäť do sveta klasického šachu – konkrétne mnohoťažiek. Slovo mnohoťažka súhrnne označuje všetky priame úlohy (teda mat niekoľkým ťahom so štandardnými pravidlami) dlhšie ako 3 ťahy. Vždy je na ťahu biely a mnohoťažku n-tým ťahom budeme označovať #n. Na prvý pohľad sa môže zdať zvláštne, prečo sú práve od štyroch ťahov všetky úlohy v jednom vreci, avšak má to dobrý dôvod (okrem toho, že by nebolo veľmi praktické mať nekonečno oddelení). Ako totiž uvidíme z príkladov, úlohy so 4 a viac ťahmi sa na seba podobajú a sú výrazne odlišné od trojťažiek, o dvojťažkách ani nehovoriac.

Je však pravda, že aj medzi mnohoťažkami máme rôzne kategórie. Ba čo viac, mnohoťažky majú zrejme najčistejšiu štruktúru delenia spomedzi všetkých oddelení s jasným rozlíšením medzi jednotlivými typmi. Existujú 3 druhy mnohoťažiek, a to:

1. logické
2. strategické
3. české

Tieto typy sa v mnohom líšia, a preto sa im budeme venovať osobitne.

Logické mnohoťažky

Slovo logické sa tu vzťahuje na to, že tieto úlohy sa podobajú na akési logické hlavolamy. Prejavuje sa to tak, že v úlohe je často množstvo zjavných jednoduchých plánov – napríklad jednoťahových hrozieb matu – na ktoré má čierny jedinú obranu. Cieľom je poskladať tieto plány do správnej postupnosti alebo urobiť nejaký úvodný manéver, ktorý ich umožní vykonať tak, že si čierny svojimi ťahmi bude škodiť, až nakoniec vyčerpá všetky možnosti obrany a hrozba zo začiatočnej pozície sa bude dať realizovať.  Najlepšie to uvidíme na príklade.

H. Grasemann, Deutsche Schachblätter, 1950, 2.cena, #6

Môžeme si všimnúť, že ak by na f5 nestál biely strelec, biely by mohol zahrať Jf5 a mat na g3 sa nedá pokryť, pretože aj po ústupe na e2 je čierny kráľ stále v pasci. Keď však skúsime strelcom ustúpiť, čierny si rozbije svoju matovú sieť (napríklad odíde strelcom z d1) a následne sa dá na útek kráľom. Biely je takto príliš pomalý.

OK, ak si teda nemôžeme dovoliť stratiť tempo, skúsme dať v prvom ťahu šach (viem, šach v prvom ťahu sa nesmie, ale predsa skúsme). Sxd3+ toho veľa nerieši, lebo po Vxd3 (hociktorá) je matová sieť rozbitá a manéver sa zas nestíha. Skúsme teda 1. Dh3+, čierny musí Ke2, avšak zas sme v tej istej situácii – nemôžeme si dovoliť stratu tempa. Nuž, neostáva nič iné, len dať znovu šach: 2. Df1+! Kxf1. Teraz už vidíme, že môžeme ustúpiť strelcom so šachom, 3. Sh3+ Ke2. Pole f5 je voľné, ale okamžité Jf5 neprináša ovocie, pretože čierny uvoľní svojmu kráľovi cestu na dámske krídlo a je po všetkom. Musíme teda šachy dotiahnúť do konca, 4. Sf1+! Kxf1, a teraz už naozaj po 5. Jf5 nie je možné mat na g3 pokryť. Bieleho hra je „logická“ v tom, že ak by čierneho pustil k ťahu, ten by mu utiekol. Tak ho jednoducho drží v šachu, až kým sa nedá vykonať rozhodujúci úder.

Vráťme sa ale k nášmu malému podvodu – ako to, že sme dali v prvom (a dokonca aj v ďalších troch!) ťahu šach? To bolo predsa jedno z hlavných pravidiel. Nuž, mnohoťažky sú raz také – pri dlhom obsahu sa toleruje aj úvodný šach. O to sú tieto úlohy ťažšie, že nemôžeme len tak vylúčiť takmer žiaden úvodník. Pravdou však ostáva, že branie silnej figúry v prvom ťahu by stále bolo považované za škaredé.

Predchádzajúca úloha síce pekne ilustruje to, že šachy sú v mnohoťažkách povolené, avšak predsa to nie je typický príklad logickej úlohy.

Hans Lepuschütz, Sahovski Vjesnik, 1951, 1. cena, #5

Hneď si môžeme všimnúť dva plány bieleho: 1. Sb6 s hrozbou 2. Dc7#, ktorá sa dá odvrátiť iba pomocou Dc3, ale najmä 1. Va8+ Dxa8 2. Sb6 Db8 a 3. De6 by bol mat, keby dáma nebola vo väzbe. Prirodzeným pokusom je preto odísť kráľom z diagonály h2-b8, ale ak zahráme jednoducho 1. Kg1, čierny vezme vežu na a7 a vyzerá to, že sa zachráni. Chcelo by to znovu, ako v predchádzajúcej úlohe, nejako získať tempo. Ako to spraviť, prezradím na konci lekcie, poviem iba, že je to vskutku netradičný spôsob zisku tempa.

Predchádzajúce dve úlohy boli o zisku tempa pre bieleho a aj keď je to jeden z klasických motívov logických mnohoťažiek, predsa len sa mi zdá, že neilustruje ich podstatu až tak dobre. Pozrime sa preto na ešte jeden príklad.

Heino Hindre, Sowjetische Mehrzügermeisters, 14. miesto, #6

Táto šesťťažka pre mňa stelesňuje všetko, čo by logická mnohoťažka mala mať, navyše zabalené do absolútne nádhernej a čistej formy. Biely má až 5 možností, kade presunúť svojho bielopoľného strelca na hlavnú diagonálu a na každý jeho ťah má čierny nejakú odpoveď – pokrytie poľa na hlavnej diagonále, na ktoré sa strelec chystá. Dokáže biely vyskladať ťahy v takom poradí, aby vynútil také čierneho reakcie, ktoré si budú navzájom zavadzať až znemožnia poslednú obranu? Odpoveď sa dozviete po vyriešení úlohy alebo na konci lekcie.

V tejto chvíli sme už slušne oboznámení s logickými mnohoťažkami a poznáme nejaké motívy, ktoré sa v nich vyskytujú, ako napríkald zisk tempa bieleho, aby si umožnil silný úder, prípadne zamotanie čiernych figúr a následný kolaps obrany čierneho. Logické mnohoťažky zvyčajne patria k tým dlhším mnohoťažkám (6+ ťahov), existujú však aj výnimky. Na druhej strane, takmer všetky dlhé mnohoťažky sú logické. Je to preto, že pre skladateľa je už neúnosné overiť nejaký neforsírovaný priebeh, ktorý trvá napríklad 8 ťahov.

Logické mnohoťažky sú veľmi príjemné na riešenie, pretože časť obsahu sa dá často vyčítať už z úvodnej pozície a… no a ťahy sú logické. Treba však dodať, že logické mnohoťažky sú zároveň aj najjednoduchším druhom mnohoťažiek. Týmto sa teda naša lekcia iba rozbieha a odteraz to už bude len horšie.

České mnohoťažky

České mnohoťažky, podobne ako aj české trojťažky, sa vyznačujú pravidlami českej úlohovej školy – teda málo bieleho materiálu, komplikované chytanie voľného čierneho kráľa a najmä modelové maty. Tu v podstate dochádza k výnimke z tvrdenia, že mnohoťažky sa líšia od trojťažiek, pretože české úlohy sa na seba dosť podobajú bez ohľadu na dĺžku. České mnohoťažky sú najčastejšie štvorťahové a okrem toho pre ne v podstate platia rovnaké pravidlá, ako pre české trojťažky – prekvapivý úvodník, ktorý často púšťa nejaké pole pri čiernom kráľovi a neforsírovaný priebeh zakončený modelovými matmi (na pripomenutie – modelové maty by mali byť v hrozbe a variantoch dokopy aspoň 3, ak sme našli menej, treba sa mať na pozore – možno chýba variant, alebo je riešenie nesprávne). Rovnako platí, že sú veľmi náročné ma riešenie. Pozrime sa teda na nejaké príklady.

Jiří Chocolous, Československý spolek Šach, Práce, 1891, #4

Typická česká úloha so všetkými rysmi, ktoré sme opísali. V duchu poučiek sa núka ako úvodník ťah niektorým jazdcom k čiernemu kráľovi. Jemne prirodzenejšie sa zdá ísť jazdcom z h4, pretože ten priamo hrozí šachmi, takže ťahy kandidáty sú Jf3 a Jf5. Teraz sa musíme pustiť do prepočtu a zistiť, či niektorý z týchto ťahov vytvára nejakú hrozbu. Po chvíli môžeme objaviť hrozbu 2. De2+ Kd5 3. Jge7# (alebo 2… Kxf5 3. De5#) po 1. Jf5, ktorá je síce krátka, ale za to s modelovým matom, a tak začneme skúmať obrany. Pri úlohe takejto náročnosti je však problém vôbec zistiť, akým spôsobom sa čierny môže brániť a čo sú obrany (obranou je len to, čo vynucuje dlhú, teda v tomto prípade 4-ťahovú, variantu – také 1… Kf3 síce bráni hrozbe, ale vychádza na to mat tretím ťahom). Nechávam to teda ako cvičenie, riešenie je ako vždy na konci lekcie.

Pri českých úlohách je veľmi dôležité objaviť úvodník a hrozbu. Tým, že je čierny kráľ taký voľný, veľa hrozieb neprichádza do úvahy, a keď už nájdeme jednu, je veľká šanca, že to bude tá správna. Žiaľ, na nájdenie hrozby a úvodníka nám neostáva nič lepšie, ako tvrdo skúšať nejaké pekné ťahy a trpezlivo prepočítavať a hľadať hrozbu.

Keďže českým úlohám sme sa venovali už pri trojťažkách a v podstate sme ich rozobrali ako sa dalo, v tejto lekcii im dáme pokoj a presunieme sa k poslednej kategórii – strategickým mnohoťažkám. Tieto sú pravdepodobne vôbec najčastejším typom mnohoťažiek a tvoria akési jadro celého oddelenia.

Strategické mnohoťažky

Názov je možno trochu mätúci a priznám sa, že aj pre mňa, pretože so stratégiou, ako ju poznáme z klasického šachu (taktika vs. stratégia), to nemá veľmi do činenia. V tomto ponímaní stratégia znamená jednoducho nejaký komplikovaný, z veľkej časti neforsírovaný a nenápadný, plán manévrov bieleho, ako dať mat čiernemu. Celkovo v kompozičnom šachu stratégia znamená niečo podobné ako obsah úlohy. To, čo je však pre nás dôležité, nie je názvoslovie, ale ako takéto úlohy vlastne vyzerajú.

W. Rudenko, Main-Post, 1974, 1.cena, #4

Vidíme, že úloha rozhodne nie je česká a zdá sa, že ani logická. Zároveň si môžeme všimnúť, že v pozícii je pripravených množstvo vodítok, ako napríklad potenciálna väzba čiernej figúry na d4, či manévre bieleho bielopoľného strelca. Je niekoľko možností, ako môžeme úlohu začať riešiť. Prvou z nich je chytiť sa kritického poľa d4. Ťahy čierneho Vxd4 a Sxd4 vyzerajú, že by to mali byť obrany, otázkou teda je, čomu tieto ťahy bránia? Odstránením pešiaka d4 sa oslabujú polia c5 a e5 – c5 je pevne kryté vežou, ale e5 by bolo voľné, keby biely prekryl svojho strelca.

Druhý smer, ktorým sa môžeme vydať je pýtať sa, ktorá figúra bude asi robiť úvodník? Biele veže a strelci nemajú veľmi ako zlepšiť svoje postavenie, Jc2 je očividne pripravený skákať na b4 a e3 po priviazaní veže resp. strelca, takže ten stojí dobre, takže ostáva Jg3 a kráľ, ktorý vyzerá, že toho veľa nezmôže. V kombinácii s predchádzajúcimi úvahami o prekrytí bieleho Sh8 by nám už mal napadnúť ťah 1. Jh5 s hrozbou 2. Jf6#. Proti tomu sú skutočne obranami Vxd4 a Sxd4 a nechávam už na čitateľa, aby našiel pokračovania za bieleho, ako aj prípadne ďalšie obrany čierneho (alebo zistil, že žiadne nie sú).

Verím, že v tí z vás, ktorí to s nami vydržali až doteraz, si už vybudovali istú vášeň pre kompozičný šach. Ak aj však náhodou nie, nasledujúca úloha určite vznieti každé šachové srdce. V nej sa zároveň ukazuje, o koľko bohatší obsah dokážu ukrývať mnohoťažky oproti trojťažkám.

Erich Zepler, Die Welt, 1956, 1. cena, 4#

Opäť vidíme, že úloha rozhodne nie je česká a ani na logickú sa až tak nepodobá. Môžeme si všimnúť, že čierny jazdec je prikovaný k svojmu miestu (hrozí mat Vd4), a teda logický pokus je napadnúť ho ťahom 1. Sh5, čierny sa však ubráni ťahom 1… e1J a po 2. Sxf3+ Jxf3 na f3 prichádza nový jazdec a čierny drží krehkú obranu. Podobne na prirodzený plán 1. Ve4 s hrozbou 2. Jxe3# (biely pokryl e5) sa čierny bráni 1… d1J 2. Jxe3+ Jxe3 a jazdec z e3 drží c4 a bráni matu. V oboch prípadoch vidíme, že keby sa čierny nebránil v prvom ťahu premenou na jazdca, tak by sa síce ubránil prvotnej hrozbe, ale v ďalšom ťahu by už dostal mat. Tu treba zbystriť pozornosť, pretože to naznačuje motív vynútenia premeny na inú figúru a následnej realizácie pôvodneho plánu (takýto motív je známy, no vyskytuje sa relatívne zriedkavo, pretože je veľmi náročné ho zložiť). Ako však prinútiť čierneho postaviť si v prvom ťahu dámu? Keďže na to, aby sme mohli realizovať pôvodné plány, musíme nechať figúry na svojich miestach, neostáva nám nič iné ako siahnuť po kráľovi. Po 1. Kb8 je a-pešiak naštartovaný na pochod do dámy, na ktorú sa premieňa priamo s matom, takže čierny je donútený postaviť si dámu na d1 alebo e1. Zvyšok riešenia je nám už známy a nechávam ho na čitateľa.

Zhrnutie

Videli sme, že medzi mnohoťažkami existujú 3 hlavné druhy a ako k nim pristupovať. Na súťaží je veľmi dôležité identifikovať typy jednotlivých úloh a ak sa medzi nimi nachádza logická, venovať sa najprv tej – pravdepodobne bude najľahšia. Ak máme tú smolu, že rozhodca vybral českú, snažme sa jej vyhýbať, kým sa dá, ale zas nie za každú cenu – možno je náhodou ľahká.

Mnohoťažkám by sme sa určite mohli venovať aj oveľa dlhšie, avšak tak, ako aj pri ostatných oddeleniach, aj tu platí, že by sme tým len odďaľovali nevyhnutné – veľa riešiť. A na vás sa už teší nová súťažná sada zapeklitých mnohoťažiek. Na záver ešte niekoľko poznámok. V prvom rade upozorňujem, že kalendár nám na tento mesiac opäť nadiktoval až 5 súťažných úloh. V druhom rade: pozorní čitatelia si možno všimli, že sme mali iba príklady úloh od 4 do 6 ťahov. Skutočne, toto sú najčastejšie typy úloh a na súťažiach sa vyskytuje zvyčajne jedna z každej dĺžky (teda jedna štvorťažka, jedna päťťažka, jedna šesťťažka). Neznamená to však, že dlhšie úlohy neexistujú. Existujú, ba dokonca sa niekedy vyskytnú aj na súťaži, je to však menej zvyčajné.

Týmto teda uzatvárame lekciu o mnohoťažkách a dostávame sa už naozaj na dohľad cieľu. V novembrovej lekcii sa pozrieme na samomaty – oddelenie úloh, kde je logika šachu postavená na hlavu ešte viac ako pri pomocných matoch – a v predvianočnom období celú našu púť zakončíme záverečnou lekciou. Želám veľa úspechov pri riešení mnohoťažiek a teším sa na ďalšie stretnutie v spoločnosti samomatov.

Riešenia príkladov

Pri riešeniach uvádzame iba varianty, ktoré dosahujú plnú dĺžku zadania (teda n ťahov pri n-ťažke) do predposledného ťahu bieleho, pretože krátkych variantov by bola často celá kopa. Nechávame na čitateľov, aby si zdôvodnili, prečo vychádzajú krátke varianty. Riešenia, ktoré píšeme sú teda v takom formáte, v akom ich treba odovzdávať, t.j. písať všetky dlhé varianty až do predposledného ťahu bieleho (rovnako ako pri trojťažkách).

1. príklad: 1. Dh3+ Ke2 2. Df1+ Kxf1 3. Sh3+ Ke2 4. Sf1+ Kxf1 5. Jf5
2. príklad: 1. Vxh4! Vxh4+ 2. Kg1 Vh8 3. Va8+ Dxa8 4. Sb6
3. príklad: 1. Sb5 Vc7 2. Sc4 fxe6 3. Sd3 Jef6 4. Se2 Jg5 5. Sf1
4. príklad: 1. Jf5
   • 1… Ve1 2. Dd4+ Kf3 3. Jgh4+
   • 1… Jxb4 2. De3+ Kd5 3. Jge7+
   • 1… gxh3 2. Jd6+Kf3 3. Je5+
5. príklad: 1. Jh5
   • 1… Vxd4 2. Je3+
     • 2… Sxe3 3. Jf4+
     • 2… Dxe3 3. Vxd4+
   • 1… Sxd4 2. Jb4+
     • 2… Vaxb4 3. Sb7+
     • 2… Vbxb4 3. Vxd4+
6. príklad: 1. Kb8
   • 1… e1D 2. Sh5 d1D/D~ 3. Sxf3+
   • 1… d1D 2. Ve4 e1D/D~ 3. Jxe3+

Súťažná úloha č. 30

BNT, mat 6-tym ťahom, úloha za max. 8 bodov

Súťažná úloha č. 31

BNT, mat 5-tym ťahom, úloha za max. 8 bodov

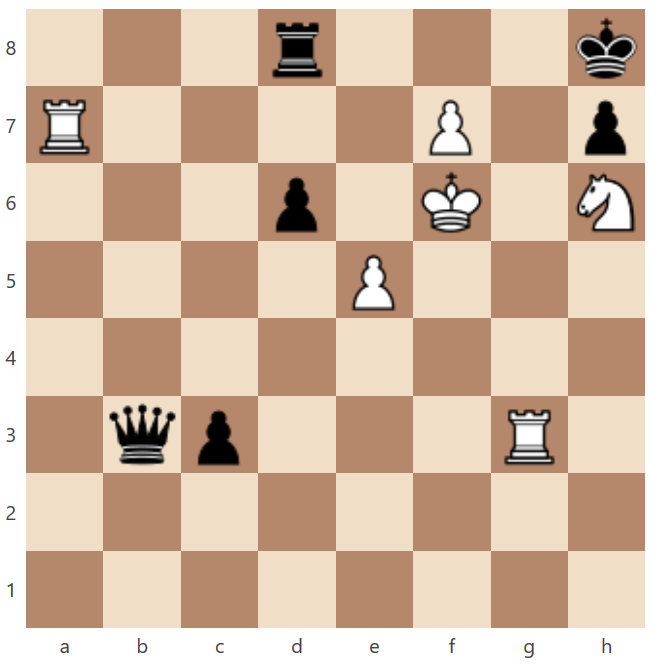
Súťažná úloha č. 32

BNT, mat 6-tym ťahom, úloha za max. 8 bodov

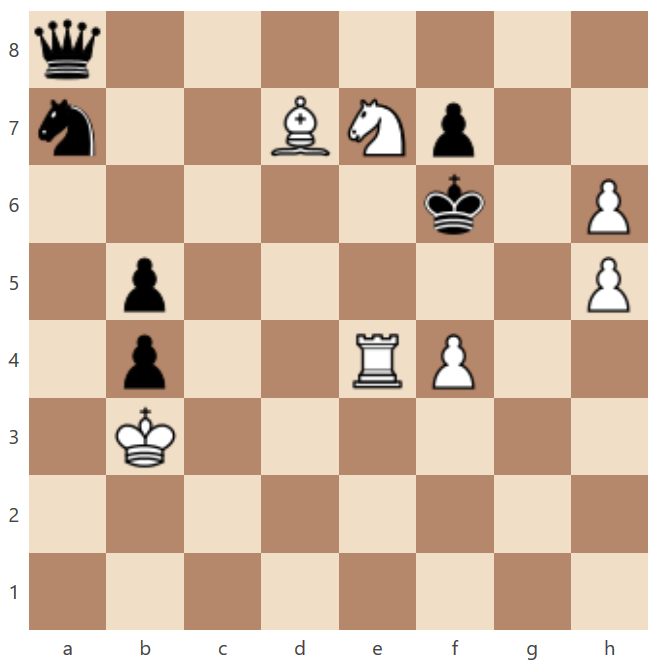
Súťažná úloha č. 33

BNT, mat 4-tym ťahom, úloha za max. 8 bodov

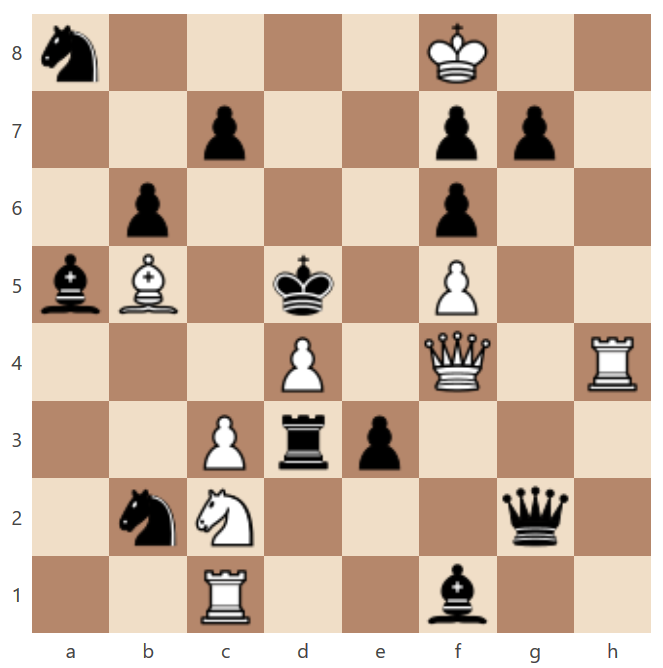
Súťažná úloha č. 34

BNT, mat 4-tym ťahom, úloha za max. 8 bodov

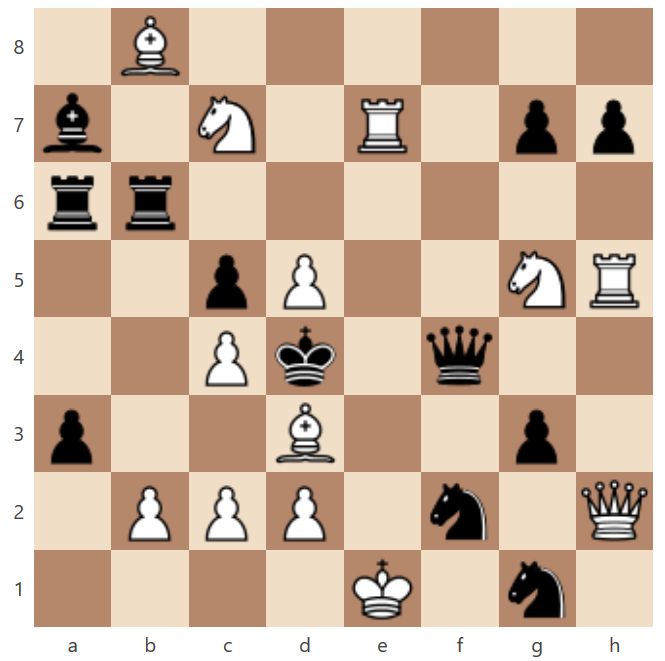
Riešenia z Lekcie 8 poslané do 6.11.2016 23:59 budú započítané do súťaže.

Riešenie pošli formulárom nižšie. Nezabudni napísať číslo súťažnej úlohy.

[contact-form-7 id=“4084″ title=“Kompozičný šach“]
Tréningové šachové DVD

Priebežné poradie po Lekcii č.7
#	      Nick	                 Počet bodov	   PH1
1	Jozef	             194	86
2	Bohuslav Czudek	     188	148
3	janjurco 	     187	131
4	OndrejFranko	     153	81
5	Peter Lukáč	     102.2	185
6	Milan Svrček	      91	119
7	PaeDr. Ján Husák     84.4	89
8	Ján Machník	     72.8	173
9	tomi	              41        160
10	Evička	              31	108
11	Stefan Galdik 	      14	41
12	Marek Tobias	     13.5	44
13	Martin Rexa	       6	35
14	Adrián Struhár	       2	81

Partneri súťaže

  

Trochu iný šach – Prológ
Trochu iný šach – Lekcia 1
Trochu iný šach – Lekcia 2 Dvojťažky
Trochu iný šach – Lekcia 3 Trojťažky
Trochu iný šach – Lekcia 4 Štúdie
Trochu iný šach – Lekcia 5 Zo života
Trochu iný šach – Lekcia 6 Svetový kongres
Trochu iný šach – Lekcia 7 Pomocné maty

[feather_follow]